

알고리즘의 시간 복잡도
프로그램의 실행 속도는 프로그램이 동작하는 하드웨어나 컴파일러 등의 조건에 따라 달라진다.
알고리즘의 성능을 객관적으로 평가하는 기준을 복잡도(Complexity)라고 한다.
복잡도는 2가지 요소를 가지고 있다.
1. 시간 복잡도(Time Complexity)
- 실행에 필요한 시간을 평가한 것
2. 공간 복잡도(Space Complexity)
- 기억 영역과 파일 공간이 얼마나 필요한가를 평가한 것
앞서 올렸던 두가지의 검색 알고리즘을 예로들어보자.
선형 검색의 시간 복잡도
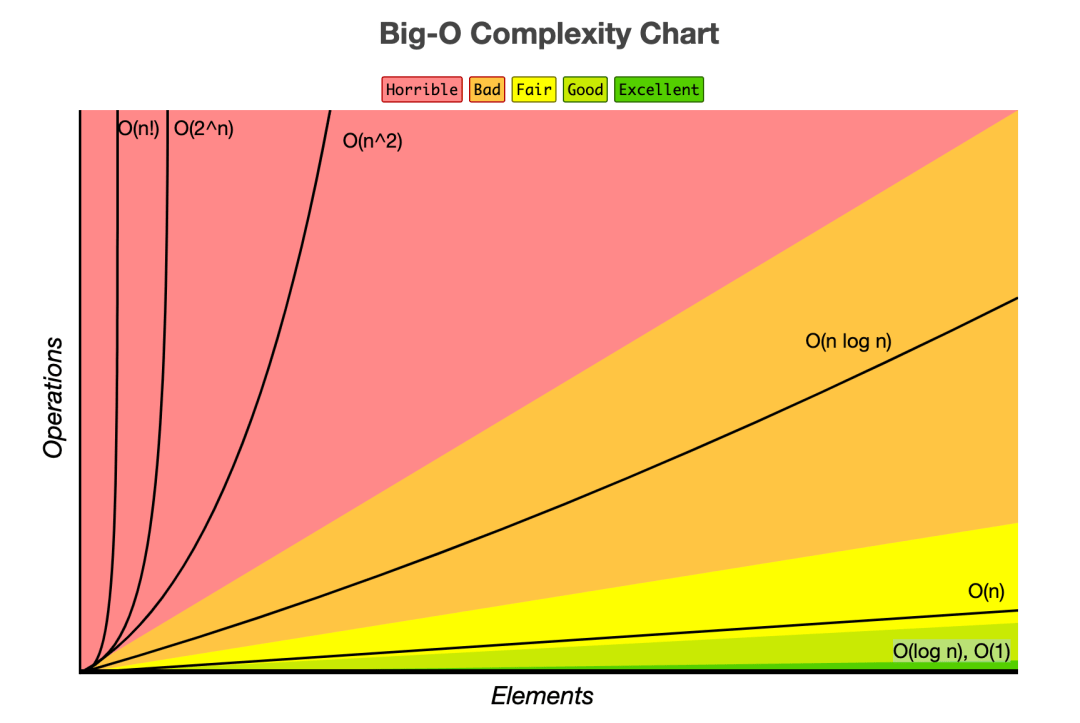
코드를 보기전에 시간 복잡도의 표기법부터 보고가자.
Big-O(빅-오) ⇒ 상한 점근 (최악)
Big-Ω(빅-오메가) ⇒ 하한 점근 (최선)
Big-θ(빅-세타) ⇒ 그 둘의 평균 (평균)
이 처럼 세가지 표기법이 있지만 알고리즘의 성능을 판단할 때의 기준을
최선이라면 얼마나 걸린다 보다는
최악에 상황에는 '이 정도까지 거릴수도 있다' 라는 것을 기준으로잡아야 대응이 가능하기 때문에
빅-오 표기법을 많이 사용한다고 한다.
int Search(const int a[], int n, int key)
{
//1 int i = 0;
//2 while(i<n){
//3 if(a[i] == key)
//4 return i; //검색 성공
//5 i++;
}
//6 return -1; //검색 실패
}n개의 요소를 가진 a라는 배열에서 key 값을 찾는 선형 검색 코드이다.
1번 처럼 변수에 값을 대입하는 경우는 처음 한 번 실행 한 이후에는 없기 때문에 O(1)로 표기한다.
하지만 2번처럼 n에 비례하여 실행이 되는 경우에는 O(n) 이라고 표기한다.
평균 실행횟수는 n /2 지만, 시간복잡도 빅오표기법은 최악의 경우를 나타내기 때문이다.
2,3,5 번줄 은 O(n)
나머지 줄은 O(1)이다.
이 알고리즘의 전체 복잡도는 차원이 가장 높은 복잡도를 선택하기 때문에
선형 검색 시간의 복잡도는 O(n)이 된다.
이진 검색의 시간 복잡도
//int형 배열 a, 배열 요소 개수 n , 찾을 키값
int Search(const int a[], int n, int key)
{
//1 int pl = 0; //배열의 맨 처음 인덱스
//2 int pr = n - 1; //배열의 마지막 인덱스
int pc; //검색 한가운데의 인덱스
do {
//3 pc = (pl + pr) / 2; //계산으로 중앙 인덱스를 구해줌
//4 if (a[pc] == key)
{
//5 return pc; //중앙값이 key값과 같다면 성공
}
//6 else if (a[pc] < key)
{
//키값이 중앙 인덱스 값 보다 크기때문에 최소인덱스를 중앙값 다음으로 바꿔줌
//7 pl = pc + 1;
}
//8 else
{
//키값이 중앙 인덱스 값 보다 작기때문에 최대인덱스를 중앙값에서 -1을 해줌.
//9 pr = pc - 1;
}
//10 } while (pl <= pr);
//최소 인덱스가 최대 인덱스보다 작을때까지만 loop
//즉 최소 인덱스값이 최대 인덱스값보다 커져버리면 실패
//11 return -1;
}
이진 검색도 마찬가지로 한번 실행되는 1,2번줄의 코드같은 경우의 시간복잡도는 O(1)이다.
하지만 3,4번과 같이 와일문이 돌때마다 실행되는 코드가 있다.
이진 검색에서 값을 찾아내는 방법은 반씩 잘라내는 방식이기 때문에 O(log n)이라고 표시한다.
log의 밑은 다른경우도 있지만 대체로 2라고 생각하면 된다고 한다.
그래서 이진 검색 알고리즘의 시간 복잡도는 가장 높은 차원인 O(log n) 이다.
함수 포인터
함수 포인터란 말 그대로 함수를 가리키는 포인터다.
하나씩 예시를 보자.
double func(int);이 경우는 매개변수를 int로 받으며 더블형 자료형을 반환하는 함수이다.
double (*func)(int);이 경우는 매개변수를 int로 받으며 더블형 자료형을 반환하는 함수에 대한 포인터이다.
double *func(int);이 경우는 매개변수를 int로 받으며 더블형 포인터를 반환하는 함수이다.
괄호의 중요성이다.
코드로 한번 구현을 해보자.
#include<stdio.h>
#include<stdlib.h>
int sum(int x1, int x2) //더하기 함수
{
return x1 + x2;
}
int mul(int x1, int x2) //곱하기 함수
{
return x1 * x2;
}
//int를 반환하는 함수에대한 포인터를 -> 매개변수로 받는 함수
void kuku(int (*calc)(int, int))
{
int i, j;
for (i = 1; i <= 9; i++)
{
for (j = 1; j <= 9; j++)
{
printf("%3d", (* calc)(i, j));
}
putchar('\n');
}
}
int main(void)
{
puts("덧셈표");
kuku(sum);
puts("\n 곱셈표");
kuku(mul);
return 0;
}
kuku함수의 매개변수를 보면 자료형 (*함수명)(매개변수) 로 적었지만,
함수에 대한 포인터는 매개변수 선언에서만 변수 이름 앞의 *와 ()를 생략한 형식으로도 선언 할 수 있다.
배열을 매개변수로 하는 함수에서 int *p를 int p[ ]로 선언하는 경우와 비슷하다.
그리고 함수 호출식의 왼쪽 피연산자는 함수 포인터가 아닌 함수 이름을 사용해도 된다.
예제에서는 printf("%3d", (* calc)(i, j)); 라고 적어놨지만 printf("%3d", calc(i, j)); 로 써도 무방하다는 얘기이다.
결과는 이렇게 나온다.
'프로그래밍 공부 > 자료구조&알고리즘 공부' 카테고리의 다른 글
| 재귀 알고리즘 / 순차곱셈 구하기, 유클리드 호제법 구현 (0) | 2022.07.16 |
|---|---|
| [디자인 패턴] 옵저버 패턴(Observer Pattern) (0) | 2022.07.12 |
| 이진 검색 알고리즘(Binary Search) (0) | 2022.07.08 |
| 선형 검색 & 순차 검색 (0) | 2022.07.06 |
| 자료구조 - 배열 (Array) (0) | 2022.06.11 |

포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!

![[디자인 패턴] 옵저버 패턴(Observer Pattern)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FLIVmc%2FbtrG5qJwOd4%2FAAAAAAAAAAAAAAAAAAAAAKsa0TSpDybWapLdwzTM3o7pPhnspk1XPSvLABTBKVXd%2Fimg.jpg%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3Dt6Bs4dSCZRlzcPxxjPZ7c40qC30%253D)
